Constraint Programming, Puzzles, ILP, and z3
Solving puzzles with computers.
Quant Out of Water
8 Posts In Total
Welcome to Quant Out of Water!
My name is Ryan and I like math – you can learn more on the “about me” page, and the motivation for writing this blog in the introduction .
All About Quadratic Forms
Quadratic forms are functions defined through symmetric matrices and represent a ubiquitous class of functions for which there is an enormous amount of useful theoretical and computational results. Indeed, in “linear-quadratic” models, it is possible to provide analytic solutions to more-or-less any question you would like to ask. This post is a tour of some foundations and results relating to quadratic forms.
Generalized Eigenvalue Problems and Trace Optimization
Most people are familiar with the concept of matrix eigenvalues. Less well known is that this concept can be fruitfully expanded to the generalized eigenvalues of pairs of matrices. Closely related are matrix trace optimization problems, which extremizes the trace of certain matrix products. Trace optimization constites a large class of practically solvable non-convex optimization problems commonly useful for dimensionality reduction and which includes the unsupervised weighted principle component analysis and the supervised method of Fisher’s Linear Discriminant. The purpose of this post is to explore some of these problems, their intuition, and their applications.
Nature's Dartboard: The Axioms of Probability
The basic axioms of probability and the idea of a random variable as a function from the sample space to \(\mathbb{R}\) are quite abstract and rather confusing at first pass. However, the axioms can be well motivated from our intuition, and defining random variables simply as functions turns out to be a brilliant and intuitive abstraction. My goal in this post is to try to explain the ideas behind the axiomatization of probability theory, and hopefully make the study of measure-theoretic probability seem a bit less intimidating.
Group Theory, Symmetry, and a Brain Teaser
I review some elementary discrete math concepts, use them to describe and solve a neat brain-teaser, and generalize the solution into a form of robust breadth first search.
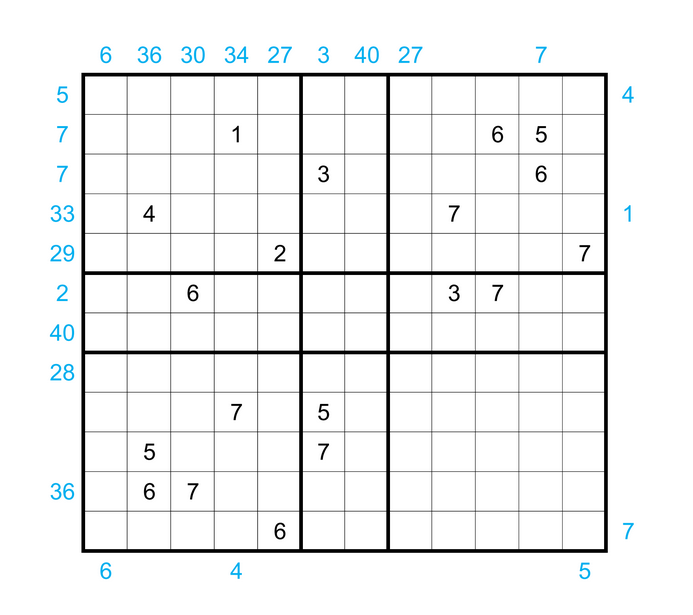
Lyapunov Stability, Linear Systems, and Semidefinite Programming
Dynamical systems are ubiquitous models occuring in science, engineering, and mathematics. Not only are they used to model real-world dynamic phenomena like the dynamics of chemical plants, population growth, and physical engineered systems, they can also be applied to model algorithms themselves. This post focuses on linear dynamical systems, their analysis by means of semidefinite programming, and connections with control theory through the computation of quadratic functionals of their paths.
Solving Equations with Jacobi Iteration
Jacobi iteration is a natural idea for solving certain types of nonlinear equations, and reduces to a famous algorithm for linear systems. This post discusses the algorithm, its convergence, benefits and drawbacks, along with a discussion of examples and pretty pictures 🖼️.
Introduction
The title of this blog, Quant out of Water, is more-or-less the first thing that came to mind. However, as I (as of 2022) work as a quant at an hedge fund, and I wanted to write a blog that was not explicitly about finance, this title reflects that motivation. I produced the fish with money using a stable diffusion model. I hope you enjoy some of my writings.
You can learn more on the “about me” page.