Constraint Programming, Puzzles, ILP, and z3

Solving puzzles with computers.

Introduction

Earlier in the year I stumbled upon a puzzle posted by Jane Street called the 4-in-1 24-7 puzzle . The puzzle is in the front matter of this post. On a first look, and on first reading through the rules for the puzzle, it appears cartoonishly complicated. But, if you’d like to take your own crack at the problem, there is a simpler 24-7 puzzle which can be solved first (as I did), before tackling the 4-in-1 version.

I’m not sure if the creators of the puzzle imagined people would print the puzzle onto paper and solve it by hand, but I immediately thought to myself: I am way too lazy for that. So instead I naturally wanted to get a computer to do all the work for me…

Throughout my short academic career, I generally took much more interest in continuous optimization than I did in discrete optimization. Almost everything I learned about discrete optimization I learned ages ago from this Coursera course , and the application of semidefinite programming to approximating MAXCUT . That being said, I knew that constraint programming was a natural approach to solving puzzles, the 24-7 puzzles being no exception.

Interestingly, I’m no stranger to algorithmic puzzle-solving. Many years ago, my girlfriend showed me an optical illusion puzzle that involved fitting a 4x4 grid of tiles with matching patterns on adjacent edges – you had to figure out how to place the tiles so that the patterns on the edges all matched.

I wrote a simple C++ program to basically brute force this puzzle – I remember running it for about a day on my ancient laptop. Armed with the tools described in this blog post, it could probably be solved in under a second, and the modeling and implementation could be done in a couple hours (rather than the whole weekend, as the C++ program probably took me).

Constraint Programming

Constraint programming is an algorithmic methodology that targets problems that have a discrete solution space, such as arranging puzzle pieces, rather than continuous problems like optimizing the shape of an aluminum can. Moreover, in contrast to optimization, the focus is upon simply finding a feasible solution that satisfies a given set of constraints, rather than optimizing an objective function subject to those constraints.

The approach involves systematically enumerating constraints that a solution must meet and which, if met, constitute a solution. A search algorithm then explores the solution space and either successfully returns a solution, or proves that one does not exist.

An example of how constraint programming might be used is in solving Sudoku puzzles. For instance, a common technique involves initially considering all numbers from 1 to 9 as candidates for each square. You then iteratively narrow down these options based on existing numbers in the grid, filling in a square when only one candidate remains and backtracking when no candidates are left. The process of checking how a decision affects the constraints is called constraint propagation and it is one particular algorithmic building block for trying to tackle constraint programming problems.

I followed a strategy like this to hack together a Sudoku solver , similarly inspired when I saw my girlfriend working on a book of Sudoku puzzles… Perhaps this is a theme 🤔 … At the time I was rather satisfied to have been able to solve Sudokus in a couple hundred milliseconds (so slow largely because of a rather inefficient representation, and writing it in Python), though there are some rather fast programs that can solve Sudoku on the order of microseconds.

These examples are ad-hoc, but I am more interested in general approaches. Similarly to how CVX makes it incredibly easy to experiment with convex optimization problems, there are general modeling tools that can be used to model and solve whole classes of discrete optimization problems. Indeed, if the constraints can be appropriately described, general purpose algorithms can be applied to search for feasible solutions.

For the rest of this post, I will describe two such general tools: Integer Linear Programming, and Satisfiability Modulo Theories, and how they can be used to solve constraint programming problems.

Integer Linear Programming

A concrete and practical means of describing constraint programs is by means of integer linear programming (ILP). Specifically, a feasibility ILP:

\begin{equation} \begin{aligned} \text{find}&\ x\\ \text{such that} &\ Ax \le b\\ &\ x_i \in \mathbb{N}_0. \end{aligned}\notag \end{equation}

This looks a lot like an ordinary linear program \(\text{min}\{c^{\mathsf{T}} x\ |\ Ax \le b, x \in \mathbb{R}^n\}\) except there is no objective (practically speaking, just set \(c = 0\)) and there is an integer constraint \(x_i \in \mathbb{N}_0\). That is, each element of the solution vector \(x\) must be an integer (including zero): \(0, 1, 2, \ldots\)

While linear programming problems are convex optimization problems, and thus entirely tractable, ILPs are NP-complete. Theoretically, there is no known “fast” algorithm for solving ILPs in general, but practically speaking, we can usually still find optimal solutions (or good suboptimal approximations) fast enough for it to be useful.

Remark (Totally Unimodular Matrices): If the matrix \(A\) in the ILP constraints is “totally unimodular”, then the LP solution and the ILP solution coincide. This is an important and tractable special case .

Another special case of ILP is what one might call Boolean Linear Programming (BLP), but is usually actually referred to as \(0-1\) linear programming. In this case, we have the constraint \(x_i \in \{0, 1\}\) (equivalent to just including the constraint \(x_i \le 1\) in the ILP). To give a sense of how powerful ILP is, the reader is encouraged to think about why the following constraints encode logical operators as BLP constraints:

• logical-and: \(z = x \wedge y\) is encoded as \(z \ge x + y - 1, z \le x, z \le y\).
• logical-not: \(z = \neg x\) is encoded as \(z = 1 - x\)

Given that we can encode AND and NOT, we can encode any Boolean expression – these operators together are universal. Here’s a couple more examples:

• logical-enforcement (if x then y): \(x \implies y\) is encoded as \(x \le y\)
• logical-implication: \(z = (x \implies y) = y \vee \neg x\): is encoded as \(z \le (1 - x) + y, z \ge 1 - x, z \ge y\)
  • This looks complicated, but is nothing but the combination of logical-or and logical-not.

The reader is encouraged to try to encode some other logical expressions, e.g., exclusive-or, logical-or, etc.

I’ll shortly use this modeling framework to encode and solve the (vanilla) 24-7 puzzle.

Satisfiability Modulo Theories

Similarly to ILP, Satisfiability modulo theories (SMT) provide a means of implementing constraint programming. SMT is a powerful methodology that generalizes Boolean Satisfiability (SAT) to allow the inclusion of arithmetic (among other things) in the constraints. For example, an instance of a SAT problem is to find a Boolean assignment to the variables \(x,y,z\) such that

\begin{equation} \begin{aligned} (x \vee \neg y \vee z) \wedge (y \vee \neg z) \end{aligned}\notag \end{equation}

evaluates to True, or prove that such an assignment does not exist.

An example of an SMT problem is to solve the (nonlinear!) system of inequalities

\begin{equation} \begin{aligned} x^2 + y^2 &> 3\\ x^3 + y &< 5 \end{aligned}\notag \end{equation}

over the integers. The inclusion of arithmetic makes SMT more general than SAT.

SAT and SMT both have rich mathematical theory surrounding them. However, I am primarily interested in SMT as a practical engineering tool, so I admit to knowing almost nothing about the theory. Indeed, I hardly know anything at all about theoretical computer science, and everything I’ve learned about SMT so far comes from this very practical book . Computationally, a library for doing SMT programming is the z3 theorem prover , which has convenient Python bindings . That same page has plenty of examples, as does this guide .

Here’s a quick example that solves the above nonlinear system:

1
2
3
4
5
6

import z3
x = z3.Int("x")
y = z3.Int("y")
z3.solve(z3.And(
    x**2 + y**2 > 3,
    x**3 + y < 5))

1

[x = -2, y = 0]

I’ll shortly use z3 to solve the complicated 4-in-1 24-7 puzzle.

Solving the Vanilla 24-7 Puzzle

Now the fun begins. Here I’m going to apply integer linear programming to solve the “vanilla” 24-7 puzzle, which looks vaguely similar to a Sudoku:

The rules are described thus:

The grid is incomplete. Place numbers in some of the empty cells below so that in total the grid contains one 1, two 2’s, etc., up to seven 7’s. Furthermore, each row and column must contain exactly 4 numbers which sum to 20. Finally, the numbered cells must form a connected region, but every 2-by-2 subsquare in the completed grid must contain at least one empty cell.

Read this over a few times – the first couple of constraints sound straightforward, but the “connected region” constraint is difficult to even wrap one’s head around. It means that the cells which are filled in need to form a connected set – there are no “islands” of numbers. We’ll see these in detail as I show how they can be encoded as constraints in an ILP.

First, I am using ortools , so let’s do some setup:

1
2
3
4
5
6
7
8

from ortools.sat.python import cp_model
from itertools import product

N = range(7)  # Grid size
K = range(1, 8)  # Values

model = cp_model.CpModel()
solver = cp_model.CpSolver()

This sets up a Constraint Programming model called model and a solver. We now just need to add our constraints!

Remark (performance): I generally first write code that is readable and easy to debug and understand, only trying to optimize when it is necessary. I’m quite directly describing the constraints of the problem, and not trying to do anything clever. I’ve introduced a number of variables which I believe add clarity, but which may, technically, be redundant. Fortunately, it is quite likely that the ILP solver is fairly capable of recognizing and eliminating obvious redundancies. That being said, the way in which a program is encoded (in any modeling language) can potentially have a significant impact on performance, so it can be worth it to revise and refactor if one is not getting the throughput they need.

Remark (modeling tip): While it may be counter intuitive, it is actually possible that increasing the number of constraints in the problem can actually improve performance. The reason being that the search space is more constrained.

The first variable I’m introducing is what I’ve called a panel. This is a \(7 \times 7 \times 7\) grid of \(\{0, 1\}\) indicators where panel[k][i][j] = 1 if and only if the cell at position (i, j) is equal to k. Let’s first encode all the static assignments using this variable.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

# Declare variables which encode the values on the board as 7 sets of Boolean indicators
panel = {k: [[model.NewIntVar(0, 1, f"z_{k}{i}{j}") for j in N] for i in N] for k in K}

# Ensure that only one of the panel indicators is active
for i, j in product(N, N):
    model.Add(sum(panel[k][i][j] for k in K) <= 1)

# Manually encode the given values
model.Add(panel[4][0][1] == 1)
model.Add(panel[6][1][2] == 1)
model.Add(panel[3][1][3] == 1)
model.Add(panel[6][1][6] == 1)
model.Add(panel[5][2][5] == 1)
model.Add(panel[5][2][6] == 1)
model.Add(panel[4][3][3] == 1)
model.Add(panel[4][4][0] == 1)
model.Add(panel[7][4][1] == 1)
model.Add(panel[2][5][0] == 1)
model.Add(panel[7][5][3] == 1)
model.Add(panel[4][5][4] == 1)
model.Add(panel[1][6][5] == 1)

The function model.Add adds a constraint to the ILP.

Notice that the constraint sum(panel[k][i][j] for k in K) <= 1, along with the fact that panel[k][i][j] is either \(0\) or \(1\), ensures that just one of these indicators can be active at a time.

Another obvious variable to introduce is the grid, which is a \(7 \times 7\) array of variables equal to the value of that cell.

1
2
3
4
5
6

# Variables that Store the value of the grid at position (i, j)
grid = [[model.NewIntVar(0, 7, f"g_{i}{j}") for j in N] for i in N]

# Encode the values of the grid from the zero-one variables
for i, j in product(N, N):
    model.Add(grid[i][j] == sum(k * panel[k][i][j] for k in K))

Since only one panel indicator can be active, sum(k * panel[k][i][j] for k in K) must be equal to the integer value that is being encoded.

This grid variable makes it easier to encode the row and column sum constraints.

1
2
3
4
5

# Each row and column must sum to 20
for row in N:
    model.Add(sum(grid[row]) == 20)
for col in N:
    model.Add(sum(grid[i][col] for i in N) == 20)

And, the reason I introduced the panel variable in the first place is because it makes is easy to encode the counting constraint:

1
2
3

# The grid must contain one 1, two 2s, three 3s, etc.
for k in K:
    model.Add(sum(sum(panel[k][i][j] for j in N) for i in N) == k)

The constraint that each row and column contain exactly four non-zero numbers, and that each \(2 \times 2\) subsquare contain an empty cell is easy to encode if we introduce another Boolean nz variable where nz[i][j] = 1 if and only if grid position \((i, j)\) is non-zero.

This variable feels redundant, as we should be able to just do things like if grid[i][j] > 0 right? Technically yes, but encoding if-else statements directly in an ILP is cumbersome and confusing – the nz variable makes reasoning easier. We’ll see later how z3 addresses this with higher level programming constructs.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

# An indicator variable for whether position (i, j) is non-zero
nz = [[model.NewIntVar(0, 1, f"nz_{i}{j}") for j in N] for i in N]

# Encode the non-zero indicator
for i, j in product(N, N):
    model.Add(grid[i][j] <= len(N) * nz[i][j])
    model.Add(nz[i][j] <= grid[i][j])

# Each row and column must contain exactly four non-zero numbers
for row in N:
    model.Add(sum(nz[row]) == 4)
for col in N:
    model.Add(sum(nz[i][col] for i in N) == 4)

# Every 2x2 subsquare must contain at least one empty cell
for i in N[:-1]:
    for j in N[:-1]:
        model.Add(nz[i][j] + nz[i + 1][j] + nz[i][j + 1] + nz[i + 1][j + 1] <= 3)

Finally, the entries need to form a connected region. This is the most difficult constraint to encode. If you are confused about what constitutes a “connected region”, take a look at the solution – you can trace a path between any two filled in digits: there are no “islands”.

One idea is to try encode this is to do some kind of connected component labeling , but it seems difficult (to me?) to encode this in an ILP such that it is both necessary and sufficient. That is, it is fairly easy to construct a set of ILP constraints which will be satisfied if there is just one connected component, but going in the other direction (that there is necessarily a single connected component when the constraints are satisfied) seems much more difficult.

An alternative method is to imagine that the cells and their neighbours form a network of pipes, and then model some kind of flow within that network. We can let each non-zero part of the grid consume a single unit of flow, and then designate one of the given filled-in cells as a source with exactly enough units of flow to cover the whole grid. Since there is one 1, two 2s, etc. up to seven 7s, we know there must be exactly 28 non-zero cells.

It is well known that flow problems can be modeled with linear programs, so this approach seems promising for our ILP. The following code does exactly this – the comments should make the code fairly clear. However, it can be subtle.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

# The maximum amount of flow
NEEDED_FLOW = 28

def _neighbours(i, j):
    if i + 1 < len(N):
        yield (i + 1, j)
    if i - 1 >= 0:
        yield (i - 1, j)
    if j + 1 < len(N):
        yield (i, j + 1)
    if j - 1 >= 0:
        yield (i, j - 1)


# Outgoing flow from cell (i, j) to neighbouring cell (p, q)
flow = [
    [
        [
            (p, q, model.NewIntVar(0, M, f"flow_{i}{j}{p}{q}"))
            for (p, q) in _neighbours(i, j)
        ]
        for j in N
    ]
    for i in N
]

# Sum up all the outgoing flow
outgoing_flow = [[0 for j in N] for i in N]
for i, j in product(N, N):
    for _, _, f in flow[i][j]:
        outgoing_flow[i][j] += f

# And separately keep track of the incoming flow
incoming_flow = [[0 for j in N] for i in N]
for i, j in product(N, N):
    for p, q, f in flow[i][j]:
        incoming_flow[p][q] += f

# Cells which are zero must have zero flow through them
for i, j in product(N, N):
    model.Add(outgoing_flow[i][j] <= M * nz[i][j])
    model.Add(incoming_flow[i][j] <= M * nz[i][j])

# Pick an arbitrary fixed node as the source
i_source, j_source = 0, 1

# Give it enough flow to fill all non-zero cells (minus itself)
model.Add(
    outgoing_flow[i_source][j_source] == NEEDED_FLOW - 1
)

# The source should have no incoming flow
incoming_flow[i_source][j_source] == 0

# Conserve flow in the network
for i, j in product(N, N):
    if i == i_source and j == j_source:
        # Except the source is unconstrained
        continue

    # non-zero cells must have positive incoming flow
    # which ensures they're connected to the source
    model.Add(incoming_flow[i][j] >= nz[i][j])

    # The outgoing flow must be one less than the incoming flow
    # i.e., each node sinks 1 unit of flow.
    model.Add(outgoing_flow[i][j] == incoming_flow[i][j] - nz[i][j])

This code looks fairly simple, but writing it was quite a challenge. It was particularly difficult to write down the right constraints that ensured only the one designated node could act as a source. In many earlier iterations I failed to properly enforce this and wound up with islands of non-zero cells. I also had a subtle bug wherein I wrote model.Add(outgoing_flow[i][j] == incoming_flow[i][j] - 1) instead of model.Add(outgoing_flow[i][j] == incoming_flow[i][j] - nz[i][j]).

Remark: When I originally solved the 24-7 puzzle (and the 4-in-1 puzzle below) I actually didn’t encode the path constraint condition. Instead, I just encoded a simpler sufficient condition and printed out all of the possible solutions (there were only 3) and selected the correct one manually – an expedient method.

In any case, we can finally print out a solution. I’ve hidden the implementation of the panel_to_str function as it is uninteresting. It just relies on getting the value of variables in the program with the method solver.Value, for example: solver.Value(panel[k][i][j]), etc.

1
2
3
4
5

if solver.Solve(model) == cp_model.OPTIMAL:
    print("Optimal solution found:")
    print(panel_to_str(panel, solver))
else:
    print("FAILED TO FIND A SOLUTION")

1
2
3
4
5
6
7
8

Optimal solution found:
7, 4, 3, 0, 6, 0, 0
0, 0, 6, 3, 5, 0, 6
0, 0, 5, 0, 5, 5, 5
0, 3, 6, 4, 0, 0, 7
4, 7, 0, 0, 0, 7, 2
2, 0, 0, 7, 4, 7, 0
7, 6, 0, 6, 0, 1, 0

And there we have it 😀

Solving the 4-in-1 Puzzle

The previous example with the 24-7 puzzle shows that ILP can be a rather cumbersome approach to encoding constraint programming problems, particularly if you endeavor to directly construct all of the linear inequalities needed to encode your program. In this section, I’m going to use the z3 theorem prover for SMT, which I think is considerably more expressive.

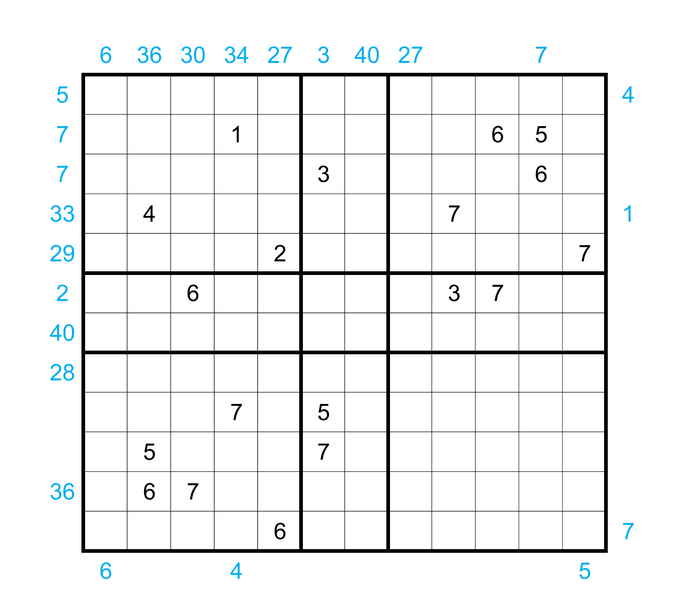
I’ll also be tackling a more difficult puzzle – the 4-in-1 24-7 puzzle. Indeed, the previous section was merely a warm up. The specific rules for the 4-in-1 puzzle is to:

Place numbers in some of the empty cells so that in total each of the four 7-by-7 outlined grids is a legal “Twenty Four Seven” grid. Namely: each 7-by-7 grid’s interior should contain one 1, two 2’s, etc., up to seven 7’s. Furthermore, each row and column within the 7-by-7’s must contain exactly 4 numbers which sum to 20. Finally, the numbered cells must form a connected region, but every 2-by-2 subsquare in the completed grid must contain at least one empty cell.

Some numbers have been placed inside the grid. Additionally, some blue numbers have been placed outside of the grids. A number outside the grid represents either the sum of the row or column it is facing, or the value of the first number it sees in that row or column.

Let’s begin!

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

import z3
from itertools import product

MAX_VAL = 7
OFFSET = 5
N = range(7)  # Subgrid size
K = range(1, 8)  # Available values
full_N = range(12)  # The whole grid

# The full grid
grid = [[z3.Int(f"x_{i}_{j}") for j in full_N] for i in full_N]

# And each of the subgrids
grids = [
    [[[grid[i + di][j + dj] for j in N] for i in N] for dj in (0, OFFSET)]
    for di in (0, OFFSET)
]

# We'll append all our constraints here
constraints = []

As before, I’m keeping track of the grid values, with a separate convenience array for the subgrids. As opposed to ILP, z3 is expressive enough that I don’t have to directly introduce multiple separate variables for different conditions like nz, panel, etc.

Constraints are set similarly, and can also be tagged. The constraints list will contain tuples of the form (tag, constraint), as the tag can be useful for debugging. You can ask z3 to print out the tags of some set of unsatisfiable constraints (whenever it finds one), so you can track down bugs more easily. Ironically, I didn’t actually make proper use of this feature, since I noticed the bug I was searching for during the process of meticulously tagging each constraint.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# Manually encode the grid
constraints.extend(
    [
        ("g[1][3] = 1", grid[1][3] == 1),
        ("g[1][9] = 6", grid[1][9] == 6),
        ("g[1][10] = 5", grid[1][10] == 5),
        ("g[2][5] = 3", grid[2][5] == 3),
        ("g[2][10] = 6", grid[2][10] == 6),
        ("g[3][1] = 4", grid[3][1] == 4),
        ("g[3][8] = 7", grid[3][8] == 7),
        ("g[4][4] = 2", grid[4][4] == 2),
        ("g[4][11] = 7", grid[4][11] == 7),
        ("g[5][2] = 6", grid[5][2] == 6),
        ("g[5][8] = 3", grid[5][8] == 3),
        ("g[5][9] = 7", grid[5][9] == 7),
        ("g[8][3] = 7", grid[8][3] == 7),
        ("g[8][5] = 5", grid[8][5] == 5),
        ("g[9][1] = 5", grid[9][1] == 5),
        ("g[9][5] = 7", grid[9][5] == 7),
        ("g[10][1] = 6", grid[10][1] == 6),
        ("g[10][2] = 7", grid[10][2] == 7),
        ("g[11][4] = 6", grid[11][4] == 6),
    ]
)

I didn’t set bounds for the variables when I constructed them, so lets do that here. Notice that z3 directly supports convenient constructs like z3.And. There is also z3.Or, z3.Implies, z3.If, and many others – pay attention for these throughout. These functions make it much easier to encode the constraints than having to reason through encoding them with ILP.

1
2
3
4
5
6
7

# Bounds for all the integers
constraints.extend(
    [
        (f"bounds_[{i}][{j}]", z3.And(grid[i][j] >= 0, grid[i][j] <= MAX_VAL))
        for i, j in product(full_N, full_N)
    ]
)

The following lengthy code block implements again the 24-7 puzzle logic, but this time in z3. Since I’ve already explained it, I don’t do so again, except for the comments in the code itself. Consider comparing this code with the ILP implementation.

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151

def encode_247_puzzle(subgrid_ix, flow_source: tuple):
    """
    The flow_source is an integer tuple for where flow originates from.
    """

    i_sg, j_sg = subgrid_ix
    subgrid = grids[i_sg][j_sg]

    def _neighbours(i, j):
        if i + 1 < len(N):
            yield (i + 1, j)
        if i - 1 >= 0:
            yield (i - 1, j)
        if j + 1 < len(N):
            yield (i, j + 1)
        if j - 1 >= 0:
            yield (i, j - 1)

    constraints = []

    # For every row and column
    for row in N:
        # They must contain exactly four non-zero numbers
        constraints.append(
            (
                f"row_count4_{i_sg}{j_sg}[{row}]",
                sum(z3.If(subgrid[row][j] > 0, 1, 0) for j in N) == 4,
            )
        )

        # And sum up to exactly 20
        constraints.append((f"row_sum20_{i_sg}{j_sg}[{row}]", sum(subgrid[row]) == 20))
    for col in N:
        constraints.append(
            (
                f"col_count4_{i_sg}{j_sg}[{col}]",
                sum(z3.If(subgrid[i][col] > 0, 1, 0) for i in N) == 4,
            )
        )
        constraints.append(
            (f"col_sum20_{i_sg}{j_sg}[{col}]", sum(subgrid[i][col] for i in N) == 20)
        )

    # Must contain one 1, two 2s, ..., seven 7s.
    for k in K:
        constraints.append(
            (
                f"counts_{i_sg}{j_sg}[{k}]",
                sum(z3.If(subgrid[i][j] == k, 1, 0) for i, j in product(N, N)) == k,
            )
        )

    # Every 2x2 subsquare must contain at least one zero
    for i in N[:-1]:
        for j in N[:-1]:
            constraints.append(
                (
                    f"2x2_{i_sg}{j_sg}[{i}][{j}]",
                    (
                        z3.If(subgrid[i][j] > 0, 1, 0)
                        + z3.If(subgrid[i + 1][j] > 0, 1, 0)
                        + z3.If(subgrid[i][j + 1] > 0, 1, 0)
                        + z3.If(subgrid[i + 1][j + 1] > 0, 1, 0)
                    )
                    <= 3,
                )
            )

    # Again implementing path connectedness by using the flow model
    # Outgoing flow from cell (i, j) to neighbouring cell (p, q)
    flow = [
        [
            [
                (p, q, z3.Int(f"flow_{i_sg}{j_sg}[{i}][{j}][{p}][{q}]"))
                for (p, q) in _neighbours(i, j)
            ]
            for j in N
        ]
        for i in N
    ]
    for i, j in product(N, N):
        for p, q, f in flow[i][j]:
            constraints.append((f"f_{i_sg}{j_sg}[{i}][{j}][{p}][{q}] >= 0", f >= 0))
            constraints.append(
                (f"f_{i_sg}{j_sg}[{i}][{j}][{p}][{q}] <= M", f <= len(N) ** 2)
            )

    # Sum up all the outgoing flow
    outgoing_flow = [[0 for j in N] for i in N]
    for i, j in product(N, N):
        for _, _, f in flow[i][j]:
            outgoing_flow[i][j] += f

    # And separately keep track of the incoming flow
    incoming_flow = [[0 for j in N] for i in N]
    for i, j in product(N, N):
        for p, q, f in flow[i][j]:
            incoming_flow[p][q] += f

    # Cells which are zero must have zero flow through them
    for i, j in product(N, N):
        constraints.append(
            (
                f"flowbal_{i_sg}{j_sg}[{i}][{j}]",
                z3.Implies(
                    subgrid[i][j] == 0,
                    z3.And(outgoing_flow[i][j] == 0, incoming_flow[i][j] == 0),
                ),
            )
        )

    # The source has exactly enough outgoing flow to fill the network
    # This time, I directly summed up the count of non-zero entries.
    i_source, j_source = flow_source
    constraints.append(
        (f"sourceinc_{i_sg}{j_sg}", incoming_flow[i_source][j_source] == 0)
    )
    constraints.append(
        (
            f"sourceout_{i_sg}{j_sg}",
            outgoing_flow[i_source][j_source]
            == sum(z3.If(subgrid[i][j] > 0, 1, 0) for i, j in product(N, N)) - 1,
        )
    )

    # Conserve flow in the network
    for i, j in product(N, N):
        if i == i_source and j == j_source:
            # Except the source is unconstrained
            continue

        # non-zero cells must have positive incoming flow
        # which ensures they're connected to the source
        constraints.append(
            (
                f"nzflow+_{i_sg}{j_sg}[{i}][{j}]",
                z3.Implies(subgrid[i][j] > 0, incoming_flow[i][j] > 0),
            )
        )

        # The outgoing flow must be one less than the incoming flow,
        # i.e., each node sinks 1 unit of flow.
        constraints.append(
            (
                f"sink+_{i_sg}{j_sg}[{i}][{j}]",
                outgoing_flow[i][j]
                == incoming_flow[i][j] - z3.If(subgrid[i][j] > 0, 1, 0),
            )
        )

    return constraints

This function is now being used as a subroutine – each subgrid needs to be a valid 24-7 puzzle. I specify the flow sources for each subgrid manually and arbitrarily from the fixed given data.

1
2
3
4
5

# Pick some arbitrary fixed nodes for the zero groups.
constraints.extend(encode_247_puzzle((0, 0), (1, 3)))
constraints.extend(encode_247_puzzle((1, 0), (0, 2)))
constraints.extend(encode_247_puzzle((0, 1), (2, 0)))
constraints.extend(encode_247_puzzle((1, 1), (0, 3)))

Now, there are some additional rules described for the 4-in-1 puzzle. Specifically, recall:

Some numbers have been placed inside the grid. Additionally, some blue numbers have been placed outside the grid. A number outside the grid represents either the sum of the row or column it is facing, or the value of the first number it sees in that row or column.

This constraint is a bit confusing, but ultimately we can just encode it with a sequence of nested if/else statements. I’ve constructed this with a recursive function as follows, but one could just as easily write down the constraints “manually” with a keyboard macro .

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

def blue_num_constraint(i: int, j: int, di: int, dj: int, num):
    """
    Starting at position i, j and moving in the direction di, dj,
    either the sum of the whole line is num OR the first non-zero
    value encountered is equal to num.
    """

    def nest_if_else(m):
        if m >= len(full_N):
            # Terminal condition: we reached the end of the row or column
            return True
        else:
            g = grid[i + m * di][j + m * dj]
            # If g > 0 then it must equal num.  Otherwise, check the next cell.
            return z3.If(g > 0, g == num, nest_if_else(m + 1))

    return (
        f"blue_[{i}][{j}][{di}][{dj}][{num}]",
        # Either the sum of the row or column is num, or we go into the nested if else
        # statements to constraint the value of the first non-zero entry.
        z3.Or(
            sum(grid[i + m * di][j + m * dj] for m in full_N) == num, nest_if_else(0)
        ),
    )

We now need to manually write down all the constraints from the figure. I enumerate them in counter-clockwise order, starting from the top-left corner.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

# Down the left side
constraints.append(blue_num_constraint(0, 0, 0, 1, 5))
constraints.append(blue_num_constraint(1, 0, 0, 1, 7))
constraints.append(blue_num_constraint(2, 0, 0, 1, 7))
constraints.append(blue_num_constraint(3, 0, 0, 1, 33))
constraints.append(blue_num_constraint(4, 0, 0, 1, 29))
constraints.append(blue_num_constraint(5, 0, 0, 1, 2))
constraints.append(blue_num_constraint(6, 0, 0, 1, 40))
constraints.append(blue_num_constraint(7, 0, 0, 1, 28))
constraints.append(blue_num_constraint(10, 0, 0, 1, 36))

# left-to-right along the bottom
constraints.append(blue_num_constraint(11, 0, -1, 0, 6))
constraints.append(blue_num_constraint(11, 3, -1, 0, 4))
constraints.append(blue_num_constraint(11, 11, -1, 0, 5))

# Up the right side
constraints.append(blue_num_constraint(11, 11, 0, -1, 7))
constraints.append(blue_num_constraint(3, 11, 0, -1, 1))
constraints.append(blue_num_constraint(0, 11, 0, -1, 4))

# right-to-left along the top
constraints.append(blue_num_constraint(0, 10, 1, 0, 7))
constraints.append(blue_num_constraint(0, 7, 1, 0, 27))
constraints.append(blue_num_constraint(0, 6, 1, 0, 40))
constraints.append(blue_num_constraint(0, 5, 1, 0, 3))
constraints.append(blue_num_constraint(0, 4, 1, 0, 27))
constraints.append(blue_num_constraint(0, 3, 1, 0, 34))
constraints.append(blue_num_constraint(0, 2, 1, 0, 30))
constraints.append(blue_num_constraint(0, 1, 1, 0, 36))
constraints.append(blue_num_constraint(0, 0, 1, 0, 6))

Finally, we instantiate and call the solver.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

def solve_constraints(constrs):
    solver = z3.Solver()

    # Add all the tagged constraints
    for tag, constr in constrs:
        solver.assert_and_track(constr, tag)

    # This will enable the solver to tell you about a subset of unsat constraints.
    solver.set(unsat_core=True)

    if solver.check() == z3.sat:
        solution = solver.model()
        print_full_grid(solution, grid)
        return solution
    else:
        print("INFEASIBLE")

        # The unsat core is some subset of unsat constraints.
        # It need not be minimal in any sense, but may be useful for
        # debugging.
        print("Unsat subset: ", solver.unsat_core())

solution = solve_constraints(constraints)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

0, 5, 0, 6, 0 | 3, 6 | 0, 0, 0, 7, 4
0, 7, 7, 1, 0 | 0, 5 | 0, 4, 6, 5, 0
0, 0, 0, 7, 5 | 3, 5 | 0, 6, 0, 6, 0
6, 4, 3, 0, 0 | 7, 0 | 5, 7, 1, 0, 0
7, 0, 0, 0, 2 | 7, 4 | 2, 0, 0, 0, 7
------------------------------------
2, 0, 6, 6, 6 | 0, 0 | 6, 3, 7, 0, 4
5, 4, 4, 0, 7 | 0, 0 | 7, 0, 6, 2, 5
------------------------------------
7, 0, 0, 0, 1 | 5, 7 | 1, 0, 0, 7, 0
0, 5, 3, 7, 0 | 5, 0 | 0, 5, 0, 4, 6
6, 5, 0, 0, 0 | 7, 2 | 0, 6, 0, 0, 5
0, 6, 7, 3, 0 | 0, 4 | 6, 6, 4, 0, 0
0, 0, 0, 4, 6 | 3, 7 | 0, 0, 3, 7, 0

Which is a correct solution! We can also check that the solution is unique by adding the negation of the solution back as another constraint and then re-solving.

1
2
3
4
5
6
7
8

constraints.append(
    (
        "soln1",
        z3.Or([grid[i][j] != solution[grid[i][j]] for i, j in product(full_N, full_N)]),
    )
)

solve_constraints(constraints)

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131

INFEASIBLE
Unsat subset:  [g[1][3] = 1,
 g[1][9] = 6,
 g[1][10] = 5,
 g[2][5] = 3,
 g[2][10] = 6,
 g[3][1] = 4,
 g[3][8] = 7,
 g[4][4] = 2,
 g[4][11] = 7,
 g[5][2] = 6,
 g[5][8] = 3,
 g[5][9] = 7,
 g[8][3] = 7,
 g[8][5] = 5,
 g[9][1] = 5,
 g[9][5] = 7,
 g[10][1] = 6,
 g[10][2] = 7,
 g[11][4] = 6,
 bounds_[0][0],
 bounds_[0][1],
 bounds_[0][2],
 bounds_[0][3],
 bounds_[0][4],
 bounds_[0][6],
 bounds_[0][7],
 bounds_[0][8],
 bounds_[0][9],
 bounds_[0][10],
 bounds_[1][0],
 bounds_[1][1],
 bounds_[1][2],
 bounds_[1][3],
 bounds_[1][4],
 bounds_[1][5],
 bounds_[1][6],
 bounds_[1][7],
 bounds_[1][8],
 bounds_[1][11],
 bounds_[2][0],
 bounds_[2][1],
 bounds_[2][2],
 bounds_[2][3],
 bounds_[2][4],
 bounds_[2][6],
 bounds_[2][7],
 bounds_[2][8],
 bounds_[2][9],
 bounds_[2][11],
 bounds_[3][0],
 bounds_[3][1],
 bounds_[3][2],
 bounds_[3][3],
 bounds_[3][4],
 bounds_[3][5],
 bounds_[3][6],
 bounds_[3][7],
 bounds_[3][8],
 bounds_[3][9],
 bounds_[3][10],
 bounds_[3][11],
 bounds_[4][0],
 bounds_[4][1],
 bounds_[4][2],
 bounds_[4][3],
 bounds_[4][5],
 bounds_[4][6],
 bounds_[4][7],
 bounds_[4][8],
 bounds_[4][9],
 bounds_[4][10],
 bounds_[4][11],
 bounds_[5][1],
 bounds_[5][4],
 bounds_[5][5],
 bounds_[5][6],
 bounds_[5][7],
 bounds_[5][9],
 bounds_[5][10],
 bounds_[5][11],
 bounds_[6][0],
 bounds_[6][1],
 bounds_[6][3],
 bounds_[6][4],
 bounds_[6][5],
 bounds_[6][6],
 bounds_[6][7],
 bounds_[6][8],
 bounds_[6][9],
 bounds_[6][10],
 bounds_[6][11],
 bounds_[7][0],
 bounds_[7][1],
 bounds_[7][2],
 bounds_[7][3],
 bounds_[7][4],
 bounds_[7][5],
 bounds_[7][6],
 bounds_[7][7],
 bounds_[7][8],
 bounds_[7][9],
 bounds_[7][10],
 bounds_[7][11],
 bounds_[8][0],
 bounds_[8][1],
 bounds_[8][2],
 bounds_[8][3],
 bounds_[8][4],
 bounds_[8][6],
 bounds_[8][7],
 bounds_[8][8],
 bounds_[8][9],
 bounds_[8][10],
 bounds_[8][11],
 bounds_[9][0],
 bounds_[9][2],
 bounds_[9][3],
 bounds_[9][4],
 bounds_[9][5],
 bounds_[9][6],
 bounds_[9][7],
 bounds_[9][8],
 bounds_[9][9],
 bounds_[9][10],
 bounds_[9][11],
 bounds_[10][0],
 bounds_[10][1],
 bounds_[10][2],
 bounds_[10][3],
 ...]

This proves that the solution I found is unique, and also serves to illustrate the “unsat subset” functionality.

Remark: You can find my name on the solution page of this puzzle, so you know I’m no fraud. But similarly as the vanilla 24-7 puzzle, I didn’t fully encode the entire problem as I’ve done now. Instead, since I only cared about getting to a final result, I manually narrowed down some of the constraints with my own direct reasoning, or through sufficient conditions, and then printed out all the candidate solutions (there were 8) with ILP. I finally found the only correct one ad-hoc, and computed the product of the areas of white space by hand.

Conclusion

We’ve seen how both Integer Linear Programming (ILP) and Satisfiability Modulo Theories (SMT), a generalization of SAT, can be used to solve constraint programming problems. These tools are incredibly powerful, and it seems likely that most practical “day to day” discrete optimization problems I might care to solve can be easily implemented and solved with ortools or z3. I find z3 to be considerably more expressive than ILP, and it is probably a good go-to tool for constraint programming. That being said, there are plenty of mathematical optimization problems which can be encoded as ILPs, so if optimization is the goal, rather than simple constraint satisfaction, ILP might be the right choice.