Group Theory, Symmetry, and a Brain Teaser

I review some elementary discrete math concepts, use them to describe and solve a neat brain-teaser, and generalize the solution into a form of robust breadth first search.

Introduction

Recently, a friend introduced me to the following brain teaser:

Problem Statement: Suppose you are kidnapped, blindfolded, and placed into a room. Your kidnappers hand you a plate with four coins on it, arranged in a $2 \times 2$ square. They will let you leave if you can flip all of the coins so that they are face up, in a finite amount of time (they ain’t got all day!). Since you can’t see, you can ask the interrogator if you’ve successfully placed all the coins heads up (if you’d like to increase the immersion, you can imagine you are actually blind, otherwise you could just take off the blindfold). The interrogator won’t lie to you, but will try to mess with you: any time the answer is “no”, they will rotate the plate before giving it back to you. The amount by which it is rotated is arbitrary – it could be random, follow a fixed pattern, or be adversarial.

The first things coming to mind with this puzzle is that you could just iterate through every possible sequence of flips, asking the interrogator whether they’re all heads up after each flip. This possibility is immediately shut down by their adversarial rotations – the interrogator can easily foil this plan.

Another possibility is through random flips. Randomization is an effective tool because the interrogator cannot determine your next move by finding a pattern in your behaviour (if you randomize effectively, even you don’t know your next move!). If you simply pick up all the coins at random, flip them randomly, and then ask if you’ve solved the puzzle, it is guaranteed (by the Borell-Cantelli Lemma ) that you will eventually stumble upon the solution. However, this is where the caveat about finite time comes in. In probability theory, it is sometimes a point of confusion what is actually meant by a random variable being finite, so let’s spell it out. If $N(\omega)$ is the number of flips taken, given a state of the universe $\omega$, the Borell-Cantelli Lemma tells us that $N(\omega) < \infty$ almost surely, so $N$ is bounded, but it is not uniformly bounded (over all possible events $\omega$). What we want is that there is some real number $N_{\text{max}} < \infty$ such that $N(\omega) \le N_{\text{max}}$ almost-surely, and this cannot be done by the random flipping strategy.

That all being said, the solution I arrived upon does not include any randomization. Before explaining the solution, I’m going to take a detour through the ideas that came to my mind, and some of the formalisms that can be used to understand the puzzle, its solution, and potential generalization.

A Mathematical Preamble

The purpose of this section is to review some mathematical formalism and terminology used in reasoning about the coins-on-a-plate puzzle. I have a limited background in discrete math or abstract algebra, so even though these concepts are rather elementary, it has been good for me to write things down. Indeed, reviewing elementary concepts facilitates Chunking (an essential part of learning ). If all one is interested in is the solution to the puzzle, or if they are already well familiar with these concepts, they can skip to Solving the Puzzle .

Equivalence Classes

In mathematics, an equivalence relation $\sim$ on a set $X$ is a binary relation satisfying the following properties:

Reflexivity: $\forall x \in X\ x \sim x$
Symmetry: $\forall x, y \in X\ x \sim y \iff y \sim x$
Transitivity: $∀ x, y, z ∈ X\ x ∼ y, y ∼ z \implies x ∼ z.$

The most famous equivalence relation is “ordinary” equality: ‘$=$’, but there are various more exotic equivalence relations: equivalence up to rotations in geometry, equivalence almost surely in probability, equivalence except on measure-zero sets in the theory of $L_p$ spaces, etc.

When dealing with a finite number of objects (finiteness is not necessary in some/many of the cases I talk about, but I keep the assumption to avoid accidentally writing something that is technically wrong for infinite sets), equivalence classes easily arise from partitions of the set. That is, if $X$ is a finite set, and $X = \bigcup_{i = 1}^M X_i$ for subsets $X_i \subseteq X$ which are all disjoint $i \ne j \implies X_i \cap X_j = \emptyset$ (i.e., the $X_i$ are a partition $X$) we can define an equivalence relation on $X$ by \[x \sim y \iff (\exists i: x \in X_i \wedge y \in X_i),\] where $\wedge$ indicates “and”. Let us quickly check that this is a bona-fide equivalence relation: Let $x \in X$. There is an $X_i$ in the partition such that $x \in X_i$ and hence “also” $x \in X_i$ verifying it is reflexive. That it is symmetric arises since $(x \in X_i \wedge y \in X_i) \iff (y \in X_i \wedge x \in X_i)$. Finally, it is transitive since the $X_i$ are a partition without any overlap: if $x, y$ are in the same set $X_i$ and $y, z$ are both in another set $X_j$, it must be that $X_i = X_j$ (and hence $x, z \in X_i$) since $y$ must be in exactly one of the $X_i$. Conversely, the reader can check that any set partition also induces an equivalence relation. Thus, set partitions and equivalence relations are equivalent.

Given an equivalence relation $\sim$ on a set $X$, the corresponding partition (i.e., the partition induced by $\sim$) is commonly denoted as $X / \sim$ as the quotient set. We then say that elements of a set in the partition (that is, elements $x \in X_i$ for some $X_i \in X / \sim$, which is a subset $X_i \subseteq X$) are equivalent up to $\sim$.

Functions, Permutations, and Groups

Any finite set with $N$ elements can be represented simply as the set of integers from $1$ to $N$ as in $X = \{1, 2, \ldots, N\}$ (a set which is commonly denoted $[N]$). It does not matter what the elements of the set actually are, you can simply refer to the first, second, etc., in an arbitrary order.

Now, what are the functions on finite sets? Well, a function $f: X \rightarrow X$ is just a mapping from some element of $x \in X$ (without loss, an integer between $1$ and $N$) to another element $f(x) \in X$. If the function is a one-to-one function (i.e., it is injective) whose domain is all of $X$, then it must also (why?) be an onto function (i.e., a surjection) and thus it is a bijection and in this context such functions are called permutations . These are nothing but re-orderings of the integers, usually denoted by $\sigma$ (or other Greek letter, instead of the more generic $f$) as in “$\sigma$ re-orders the sequence $(1, 2, \ldots, N)$ into $(\sigma(1), \sigma(2), \ldots, \sigma(N))$”.

Since permutations are bijections, they have an inverse. Moreover, the composition operation amongst permutations is associative (why?): for permutations $\sigma, \pi, \tau$ on $X$, it is the case that $(\sigma \circ \pi) \circ \tau = \sigma \circ (\pi \circ \tau)$, where, e.g., $(\sigma \circ \pi)(x) = \sigma(\pi(x))$. This means that (with the trivial “doing nothing” permutation $Id(x) = x$ serving as the identity) the set of all permutations of $X$, call it \[G_X = \{\sigma: X \rightarrow X\ | \ \sigma \text{ is a bijection}\},\] along with the composition operation constitutes a (finite) Group $(G_X, \circ)$. This particular group $G_X$ of all bijections is particularly special, and is referred to as the Symmetric Group $S_N$ on $N$ elements – it is worthwhile noting that the size of this group grows rather quickly: there are $N!$ bijections in $S_N$.

Cycles and Decomposition

Given a permutation $\sigma \in S_N$, an $r$-cycle is a sequence of $r \ge 1$ numbers $i_1, \ldots, i_r$ such that $i_{k + 1} = \sigma(i_k)$ and $i_r = i_1$. Given an $r$-cycle of $\sigma$, we can collect each $i_1, \ldots, i_r$ into a set $C \subseteq [N]$ called an orbit and restrict $\sigma$ to this cycle so that $\sigma_C$ is equal to $\sigma$ in $C$, and the identity outside of $C$ as in $\forall x \in C:\ \sigma_C(x) = \sigma(x)$ and $\forall x \in C^{\mathsf{c}}:\ \sigma_C(x) = x$. Remarkably, permutations can be decomposed into a composition of their cycles:

Theorem (Cyclic Decomposition): Let $\sigma \in S_N$. Then, there exists a partition $C_1, \ldots, C_m$ of $[N]$ such that $\sigma = \sigma_{C_1} \circ \cdots \circ \sigma_{C_m}.$ Moreover, each $C_i$ is an orbit of a cycle of $\sigma$, and for any cycle of $\sigma$ there is a corresponding orbit $C_i$.

proof (sketch): Since $\sigma$ acts on a finite set, there exists at least one cycle, call its orbit $C_1$. We have the partition $[N] = C_1^{\mathsf{c}} \cup C_1$ and the decomposition $\sigma = \sigma_{C_1^{\mathsf{c}}} \circ \sigma_{C_1}$ since $\sigma_{C_1}(x) = x$ on $C_1^{\mathsf{c}}$. Now, $C_1$ contains at least one element, and $\sigma_{C_1^{\mathsf{C}}}$ is another permutation when restricted to $C_1^{\mathsf{c}}$, so the theorem follows by induction. $\square$

From the partitioning of $[N]$ by the orbits of a permutation, we see that any permutation also induces a collection of equivalence classes (exactly the orbits of the permutation)! Within each of these equivalence classes, we can say that the elements are identical up to the operation of $\sigma$. As well, we say that any set $C$ such that $x \in C \implies \sigma(x) \in C$ is invariant to $\sigma$ – clearly, the partitions induced by $\sigma$ are all invariant sets. These formalisms can be used to understand the structure of the coins-on-a-plate puzzle.

Solving the Puzzle

The main idea for solving the puzzle revolves around identifying particular partitions of the set of all states of the game, thus identifying equivalence relations. I then define some natural operations that one can apply to the coins on the plate and reason about how those operations map elements of one equivalence class into another. It turns out that we can apply these operations in a particular order such that we are guaranteed to eventually reach the solution.

Representation and Rotations

Abstractly, we can represent the state of each coin as either being heads $H$ or tails $T$. Since the coins are arranged in a square, we can think of the state of the whole puzzle as being the sequence of states of each individual coin following a left-to-right and top-to-bottom ordering. Notice that we’ve already encountered an equivalence class: we naturally think of aligning the coins to look as though they are on a “right-angle” when facing us – following this convention, a whole set of angles of the plate spanning $90^\circ$ ($45^\circ$ in either direction) all represent equivalent configurations. If the interrogator rotates the plate by, say, $37^\circ$ before handing it back to us, we should be able to feel around the coins to rotate this back to $0^\circ$. Thus, when we speak of an arrangement of coins on the plate, we are already really speaking of a whole equivalence class, all of which are equivalent up to rotation back to the nearest right-angle alignment of the coins. The upshot here is that listing the coins in this order results in a finite representation of the set of all possible states (of which there are $2^4 = 16$) as elements of the set \[S = \Bigl\{{HH \atop HH}, {TH \atop HH}, {HT \atop HH}, \ldots, {TT \atop TH}, {TT \atop TT}\Bigr\},\] which is naturally isomorphic (i.e., equivalent) to the set $[16] = \{1, \ldots, 16\}$.

Any such rotation operation can now naturally be thought of as a permutation $\texttt{rotate}^n$, where $n$ indicates the number of $90^\circ$ angles the plate is clockwise rotated. For example, $\texttt{rotate} \Bigl({HT \atop HH}\Bigr) = {HH \atop HT}$ and $\texttt{rotate}^2 \Bigl({HT \atop HH}\Bigr) = {HH \atop TH}$, etc. The power notation with $n$ is naturally suggestive since $n$ rotations by $90^\circ$ is equivalent to applying the single $\texttt{rotate}$ permutation $n$ times. Since we don’t know how many times the interrogator will apply $\texttt{rotate}$ before giving us the plate back, we need to work with equivalence classes of states which are equivalent up to the action of this permutation.

Remark: It is an exercise for the reader to enumerate all of the equivalence classes induced by $\texttt{rotate}$. I should note at this point though that I stumbled upon the appropriate sets and operations for solving the puzzle through intuition, and only went backwards afterwards to add some formalism. In my experience, this is typical of mathematical problem solving and research – you begin by understanding and solving particular problems and special cases ad-hoc through intuition, and then go back to formalize the ideas, which opens up new ideas and generalizations, which you begin by solving ad-hoc, and then later formalize, which leads to more questions…

Solved States

The next key observation involves another permutation and collection of equivalence classes. Consider a $\texttt{flip\_all}$ operation – you can apply this operator to the coins on the plate by flipping every coin onto its other face. Since this $\texttt{flip\_all}$ operation is just a permutation, it decomposes the space $S$ into equivalence classes (whose elements are all equivalent up to the operation of $\texttt{flip\_all}$). Examples include $\Bigl\{ {HT \atop HT}, {TH \atop TH} \Bigr\}, \Bigl\{ {HT \atop TH}, {TH \atop HT} \Bigr\}$, etc, which are all orbits containing just two elements. Another important example is \[S_\star = \Bigl\{{HH \atop HH}, {TT \atop TT}\Bigr\},\] which is the equivalence class (of $\texttt{flip\_all}$) containing the solved state ${HH \atop HH}$. The importance of this class arises as follows.

Consider the following query, which I’ll refer to as $\texttt{solved?}(s)$: Ask the interrogator if the puzzle in state $s$ is solved. If it is, you’re done. If not, the plate is returned to you after application of some number of $\texttt{rotate}$ permutations. Now, consider the composite query ($\texttt{solved?}(s)$ is not formally a permutation, so I use the word “query”): $\texttt{solved?} \circ \texttt{flip\_all}$, which in words describes: first flip all the coins onto their other side and then ask the interrogator if the puzzle is solved. Therefore, since $\texttt{rotate}$ does not change the number of heads or tails in the configuration (i.e., both elements of $S_\star$ are fixed-points of $\texttt{rotate}$) if you reach a state $s \in S_\star$ then you can first query $\texttt{solved?}$ and if the plate is returned to you (which means you must have asked about the configuration ${TT \atop TT}$) then you know that the state $s$ has not changed and you can apply the composite query $\texttt{solved?} \circ \texttt{flip\_all}$ which is now guaranteed to result in successfully solving the puzzle.

Thus, if you do this every time you want to know if the puzzle is solved, then you have effectively solved the puzzle anytime all of the coins are all face up, or all face down – if they are face down, then they will be face up the second time you ask. Thus, the two states in $S_\star$ “coins all face up” and “coins all face down” form an equivalence class of “solved states” according to the composite query described above – I’ll call this composite query $\texttt{solved?}^\star$. We can now frame our problem as reaching any state in $S_\star$.

Three More Equivalence Classes

Consider the following three sets: \[S_1 = \Bigl\{{HH \atop HT}, {HH \atop TH}, {HT \atop HH}, {TH \atop HH}, {TT \atop TH}, {TT \atop HT}, {TH \atop TT}, {HT \atop TT}\Bigr\},\] which has either a single head or a single tail; \[S_2^{(d)} = \Bigl\{{HT \atop TH}, {TH \atop HT}\Bigr\},\] with two heads and two tails arranged diagonally from one and other; and \[S_2^{(s)} = \Bigl\{{HH \atop TT}, {HT \atop HT}, {TT \atop HH}, {TH \atop TH}\Bigr\},\] consisting again of two heads and two tails, but now sitting side-by-side. Critically, the sets we have so far defined form a partition of the space: \[S = S_\star \cup S_1 \cup S_2^{(s)} \cup S_2^{(d)},\] and thus more equivalence relations given by membership in these sets. Moreover, each of these sets is invariant to both permutations $\texttt{rotate}$ and $\texttt{flip\_all}$. Indeed, $S_2^{(d)}$ is exactly one of the equivalence classes induced by both, $S_2^{(s)}$ is an equivalence class induced by $\texttt{rotate}$ and is the union of two equivalence classes of $\texttt{flip\_all}$, and $S_1$ is the union of two equivalence classes of $\texttt{rotate}$ along with the corresponding ones of $\texttt{flip\_all}$. Since the elements of the sets are all equivalent to one and other (in the sense of being members of a partition, and in the sense of rotational symmetry) we can treat all members of the class simultaneously. These sets, along with three more operations, will allow us to formalize a solution to the puzzle.

Due to the invariance of these sets to the $\texttt{rotate}$ permutation, the action of the rotation introduced by the interrogator when you query $\texttt{solved?}$ does not have any affect on the membership of $s$ in one of these sets. This is, of course, not true of any arbitrary subset of $S$, and hence the choice of sets above is in some sense “cunning” (and now we see, well motivated by the consideration of equivalence classes!). Indeed, rotations applied to $\tilde{S} = \{{HH \atop TT}, {TT \atop HH}\}$ could produce something in $\tilde{S}$, but it could also produce something in $\{{HT \atop HT}, {TH \atop TH}\}$!

More Permutations on $S$

The additional permutations we need to solve the puzzle are: $\texttt{flip\_one}$, which flips over an arbitrary single coin; $\texttt{flip\_side}$, which flips over two side-by-side coins; and $\texttt{flip\_diag}$, which flips over arbitrary cross-diagonal coins. These functions are not uniquely defined (e.g., which coin do you flip over for $\texttt{flip\_one}$) but the choice of which particular permutation you use does not matter, so I’m glossing over this.

We can reason through the effects of how these map between our equivalence classes as follows (I skip the consideration of how $S_\star$ is affected since we will always query $\texttt{solved?}^\star$ between each operation, so if we hit $S_\star$ we are done):

\begin{equation} \begin{aligned} \texttt{flip\_one}: S_1 \rightarrow S_2^{(d)} \cup S_2^{(s)} \cup S_\star\\ \texttt{flip\_one}: S_2^{(d)} \cup S_2^{(s)} \rightarrow S_1, \end{aligned} \end{equation}

since if $s \in S_1$ and we flip over a single coin, then we must now have either two heads and two tails, or we happened to flip over the “right” coin and reach a solved state. Alternatively, if we begin with two $H$s and two $T$s, then flipping one coin over necessarily puts us back in $S_1$ with either three $H$s and one $T$, or three $T$s and one $H$. For the side-by-side flip operator:

\begin{equation} \begin{aligned} \texttt{flip\_side}: S_1 \rightarrow S_1\\ \texttt{flip\_side}: S_2^{(d)} \rightarrow S_2^{(s)}\\ \texttt{flip\_side}: S_2^{(s)} \rightarrow S_\star \cup S_2^{(d)}, \end{aligned} \end{equation}

since if there is one head (or one tail), application of $\texttt{flip\_side}$ must necessarily result in three heads or tails; if there are heads diagonal from one and other (i.e., $s \in S_2^{(d)}$) then $\texttt{flip\_side}$ must necessarily flip one head and one tail, and thus result in side-by-side heads and tails; and if $s \in S_2^{(s)}$ then we either get lucky and flip the “right” coins into a solved state, or we flip the “wrong” coins into a diagonal state $S_2^{(d)}$. Finally, for the diagonal flipping operator:

\begin{equation} \begin{aligned} \texttt{flip\_diag}: S_1 \rightarrow S_1\\ \texttt{flip\_diag}: S_2^{(d)} \rightarrow S_\star\\ \texttt{flip\_diag}: S_2^{(s)} \rightarrow S_2^{(s)}, \end{aligned} \end{equation}

by similar reasoning. This is the key to the puzzle. If we are faced with some $s \in S_2^{(d)}$, then application of $\texttt{flip\_diag}$ is guaranteed to place us into the solved state $S_\star$. The only difficulty now is that we cannot know whether or not $s \in S_2^{(d)}$! Regardless, this feels like progress.

Transition Diagramming

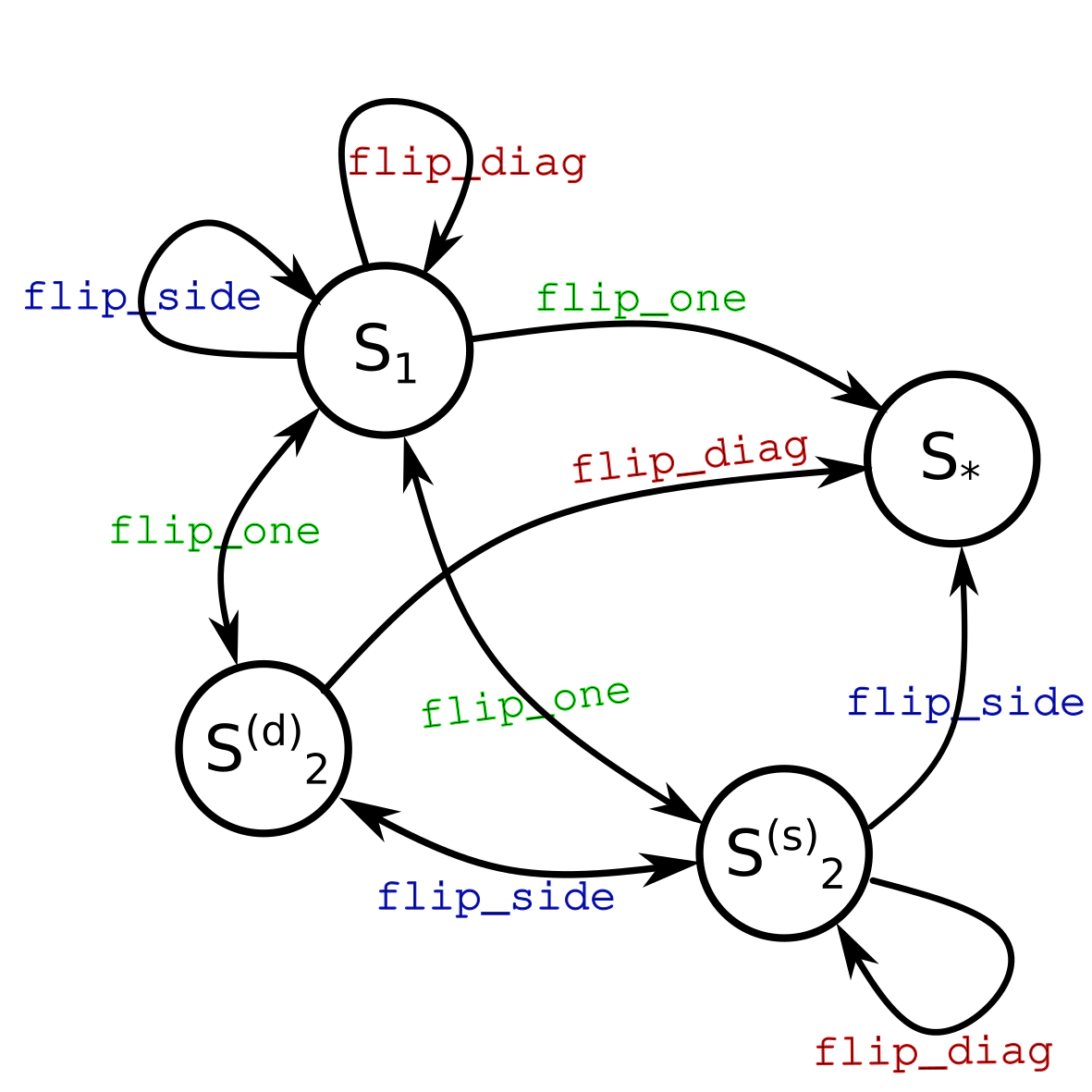
The simple enumeration of the action of the operators $\texttt{flip\_one}, \texttt{flip\_side}, \texttt{flip\_diag}$ on the sets $S_1, S_2^{(s)}, S_2^{(d)}$ described in the previous section can be difficult to visualize. Our intuition is that we should try to find some appropriate order in which to apply these operations which will guarantee that we eventually reach the state $S_\star$, but how? We can make progress towards this task by drawing a diagram of all the possible transitions:

Figure 1: Transition Diagram for each Function and Set

One thing we can notice from this diagram is that some operations map from a set and back into itself, i.e., some of the sets described above are also invariant to $\texttt{flip\_diag}$ or $\texttt{flip\_side}$. For example, $\texttt{flip\_diag}$ maps from $S_2^{(s)}$ back into itself, as well as from $S_1$ and back into itself. Recall that there is also an implicit self-loop corresponding to the $\texttt{rotate}$ permutation for each set, i.e., we can safely ask if the puzzle is solved (following the logic described in Solved States ) without the interrogator being able to effect the state we are in.

A Solution

Using the diagram above, we can deduce a solution to the puzzle. Start in any arbitrary state $s \in S$: first, make the $\texttt{solved?}^\star$ query, if $s \in S_\star$ then we are done (that was easy!), otherwise, we are in a state \[s \in S \setminus S_\star = S_1 \cup S_2^{(d)} \cup S_2^{(s)}.\] Apply the operator $\texttt{flip\_diag}$ and then query $\texttt{solved?}^\star$ again. If we happened to be in $S_2^{(d)}$, then the puzzle is solved, otherwise (notice the self-loops) we must be in $s \in S_2^{(s)} \cup S_1$. Now, apply $\texttt{flip\_side}$, followed by $\texttt{solved?}^\star$, $\texttt{flip\_diag}$, and $\texttt{solved?}^\star$ again. If we were in $S_2^{(s)}$, then $\texttt{flip\_side}$ transitioned us into $S_2^{(d)}$, and $\texttt{flip\_diag}$ brought us into $S_\star$. If we were in $S_1$, then we are still in $S_1$, since this set is invariant to both $\texttt{flip\_diag}$ and $\texttt{flip\_side}$. To solve the puzzle from here, we apply $\texttt{flip\_one}$ and query $\texttt{solved?}^\star$. If that query failed, then we must be in $S_2^{(d)} \cup S_2^{(s)}$ in which case we can apply $\texttt{flip\_diag}$ and query $\texttt{solved}?^\star$, which will finish the puzzle if we were in $S_2^{(d)}$. Otherwise, we are in $S_2^{(s)}$ and applying $\texttt{flip\_side}$ followed by $\texttt{solved?}^\star$ and then again $\texttt{flip\_diag}$ which is finally guaranteed to place us into $S_\star$, wherein a final $\texttt{solved?}^\star$ query is the end.

We have solved the puzzle – regardless of our starting position, and regardless of how random or adversarial are the rotations to the plate of coins done by the interrogator (they can even know our exact plan!), the above policy will eventually move us into the solved state $S_\star$. To summarize the policy, we apply the following order of operations, querying $\texttt{solved?}^\star$ between each operator: $\texttt{flip\_diag}, \texttt{flip\_side}, \texttt{flip\_diag}, \texttt{flip\_one}, \texttt{flip\_diag}, \texttt{flip\_side}, \texttt{flip\_diag}$.

Computational Generalizations

Solving this particular brain-teaser is satisfying, but a solution is not a good solution to me unless it is illustrative or indicative of a more general pattern. Indeed, I wrote out the formalism above exactly for the purpose of trying to reason through a more general idea. To introduce the idea, suppose we have $N$ states $V = [N] \overset{\Delta}{=} \{1, 2, \ldots, N\}$ and $K$ functions $\mathcal{F} = \{f_k: V \rightarrow V\ |\ k \in [K]\}$ on $V$. Given this data, we can define a graph $\mathcal{G} = (V, \mathcal{E})$ where the set of vertices is naturally $V$ and the edges are tuples $\mathcal{E} \subseteq \{(i, j, f)\ |\ i, j \in V, f \in \mathcal{F}\}$ where the edges $(i, j, f) \in \mathcal{E}$ is present in the graph if there is a function $f \in \mathcal{F}$ which maps from node $i$ to node $j$. Each node will have $K$ edges emanating from it – one for each function. Let’s suppose as well that there is a fixed target state $s^\star \in S$ and that this state is invariant to every function application $f_k(s^\star) = s^\star$, i.e., when we reach the target state, we know it. This graph is analogous to the graph I drew for the coin problem.

Now, the interesting part of this comes in when we suppose we do not know what state we are in. The new question is: can we find a search algorithm which will find a sequence of functions leading to a goal state, but which does not require knowledge of what vertex it is currently visiting? Abstractly, given a target state $s^\star$, can we find a finite (ideally minimal) sequence of functions $f_1, f_2, \ldots, f_M \in \mathcal{F}$ which when applied from an arbitrary starting point, are guaranteed to eventually reach the target state $s^\star$?

Uncertain Breadth First Search

There may exist a better algorithm, but this problem can be solved by means of breadth first search. However, we cannot just apply BFS directly upon the graph $\mathcal{G}$, since we don’t know our starting point. Instead, we’ll apply BFS on a graph over the power set $2^V$ of $V$ (i.e., the set of all subsets of $V$). We generalize the application of $f \in \mathcal{F}$ to act on $2^V$ by the definition \[ W\subseteq V:\ f(W) = \{f(w)\ |\ w \in W\},\] i.e., we apply $f$ to every element of the subset. This gives us an edge relation for a graph $\mathcal{G}^\star = (2^V, \mathcal{E}^\star)$: we have \[(U, W) \in \mathcal{E}^\star \iff \bigl(\exists f \in \mathcal{F}:\ f(U) = W\bigr).\] The goal is to find a path through this “power-graph” leading to the state $S_\star = \{s^\star\}$, the singleton set containing only the goal state.

A completely hacked-together implementation of this idea for the coins-on-a-plate problem is given here:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59


import typing as ty

from functools import reduce
from collections import deque

# Some nicer names for the nodes in the graph
Node = str
S1: Node = "S1"
S2d: Node = "S2d"
S2s: Node = "S2s"
S_star: Node = "S_star"

TransitionFunction = ty.Callable[[Node], ty.Set[Node]]

# To easily keep track of what has been visited
def _hash(s: ty.Set[Node]):
    return hash("".join(str(hash(n)) for n in s))

# Computes the set of next nodes obtained by applying `op` from some uncertainty set
def _next_nodes(nodes: ty.Set[Node], op: TransitionFunction):
    return reduce(lambda acc, new_nodes: acc | new_nodes, (op(w) for w in nodes), set())

# The robust implementation of BFS
def uncertain_bfs(nodes: ty.Set[Node], ops: ty.Dict[str, TransitionFunction]):
    visited = {_hash(nodes)}
    queue = deque([(("START",), nodes)])
    while queue:
        path, nodes = queue.pop()
        for name, op in ops.items():
            new_nodes = _next_nodes(nodes, op)
            if (hsh := _hash(new_nodes)) not in visited:
                visited.add(hsh)
                queue.append(((*path, name), new_nodes))
            if new_nodes == {S_star}:
                print(f"SUCCESS: {(*path, name)}")
                return
    print("FAILURE!")

# Helper to make transition functions with S_star being an absorbing state
def _make_op(mapping: ty.Dict[Node, Node]) -> TransitionFunction:
    def op(v: Node) -> ty.Set[Node]:
        if v == S_star:
            return {S_star}
        return mapping[v]
    return op

# The operations on the coins
flip_diag = _make_op({S1: {S1}, S2d: {S_star}, S2s: {S2s}})
flip_side = _make_op({S1: {S1}, S2d: {S2s}, S2s: {S2d, S_star}})
flip_one = _make_op({S1: {S2d, S_star, S2s}, S2d: {S1}, S2s: {S1}})

# The possible starting positions
nodes = {S1, S2d, S2s, S_star}

# And names for the transition functions
transition_functions = {"flip_diag": flip_diag, "flip_one": flip_one, "flip_side": flip_side}

# Which we finally run the algorithm on
uncertain_bfs(nodes, transition_functions)

\[\texttt{SUCCESS: (‘START’, ‘flip\_diag’, ‘flip\_side’, ‘flip\_diag’, ‘flip\_one’, ‘flip\_diag’, ‘flip\_side’, ‘flip\_diag’)}\]

And indeed, this code outputs the same policy I came up with ad-hoc in the previous section.

Conclusion

I thought that the puzzle described at the beginning of this article was very neat and wanted to write down a complete solution. We saw how the idea of symmetries were crucial for solving the puzzle, and that these symmetries can be described through the language of equivalence classes. Moreover, the remarkable cyclic decomposition theorem for permutations (nothing but bijections on finite sets) tell us that we can partition all the possible states of the coins on the plate into a collection of cycles and equivalence classes. Some of these sets are invariant to certain operations on the coins, and therefore create self-loops in a graph describing how the state of the puzzle evolves. Diagramming this graph allowed us to write down an ad-hoc solution to the coins-on-a-plate puzzle.

The idea of searching in a graph when you don’t know your starting point generalized to a form of robust breadth-first search. In this algorithm, we keep track of an entire uncertainty set of nodes that we can plausibly be, and stop once that set contains nothing but the goal state. I have few ideas for what such an algorithm might be practically useful for, but there it is!